UMIUMI
METHOMIKA: Jurnal Manajemen Informatika & Komputerisasi AkuntansiMETHOMIKA: Jurnal Manajemen Informatika & Komputerisasi AkuntansiK-Means tradisional menghadapi 2 (dua) permasalahan utama, yaitu: Penentuan Centroid Awal dan Cluster Awal yang kurang baik. Penentuan centroid awal dengan menggunakan bilangan acak merupakan salah satu permasalahan utama pada K-Means klasik yang mengakibatkan akurasi rendah dan waktu komputasi yang lama. Begitu pula penentuan centroid yang baik dari setiap cluster tanpa disertai proses memperhatikan performa dari setiap cluster juga dapat menyebabkan nilai akurasi yang diperoleh kurang baik. Penelitian ini akan memberikan kontribusi tentang bagaimana performa yang diperoleh dari penentuan centroid awal yang baik dikombinasikan dengan penggunaan cluster yang baik. Penentuan centroid awal yang baik dilakukan dengan menggunakan K-Means Grid Mapping yang membagi penentuan centroid ke dalam beberapa Grid Point. Hasil dari penelitian ini adalah gabungan antara Iterative K-Means dengan Grid Mapping K-Means sehingga menjadi Iterative Grid Mapping K-Means yang akan mendapatkan centroid awal yang baik dan juga cluster yang baik seperti yang ditunjukkan pada tabel iris dan abalone, perbandingan variabel pada iris dan abalone mempengaruhi cluster yang paling baik sebagai hasilnya.
Dalam penelitian ini, kontribusi yang diberikan adalah sebagai berikut, hasil pengujian menunjukkan bahwa Iterative Grid Mapping K-Means memberikan hasil yang lebih baik dibandingkan dengan Iterative K-Means dan Iterative Grid Mapping K-Means.Peningkatan jumlah iterasi dapat meningkatkan kinerja masing-masing metode, baik dari segi nilai Average Precision maupun Best Precision.Jumlah instance dan atribut dalam dataset dapat mempengaruhi kinerja masing-masing metode yang menunjukkan bahwa kinerja masing-masing metode lebih baik pada dataset Iris dibandingkan dengan dataset Abalone.
Penelitian yang telah dilakukan ini berhasil menunjukkan bahwa metode Iterative Grid Mapping K-Means menawarkan peningkatan akurasi dalam clustering data. Namun, ada beberapa arah penelitian lanjutan yang dapat dieksplorasi untuk lebih menyempurnakan dan memperluas manfaat metode ini. Pertama, akan sangat berharga untuk menyelidiki secara mendalam bagaimana Iterative Grid Mapping K-Means berkinerja dari segi efisiensi komputasi dan skalabilitas ketika diterapkan pada dataset yang jauh lebih besar dan kompleks dibandingkan dengan dataset Iris atau Abalone. Studi ini bisa mengukur waktu eksekusi dan penggunaan sumber daya untuk memahami apakah keuntungan akurasi juga diiringi oleh efisiensi yang memadai pada skala data yang masif, serta mengidentifikasi potensi bottleneck dan optimasi algoritma lebih lanjut. Kedua, salah satu tantangan utama dalam implementasi K-Means adalah penentuan jumlah cluster (nilai K) yang optimal. Oleh karena itu, penelitian di masa depan dapat berfokus pada pengembangan atau pengintegrasian mekanisme otomatis ke dalam Iterative Grid Mapping K-Means untuk menemukan nilai K terbaik tanpa intervensi manual, mungkin dengan memanfaatkan indeks validitas cluster yang canggih atau pendekatan berbasis ensemble. Terakhir, perlu juga dipertimbangkan bagaimana metode ini dapat diadaptasi atau ditingkatkan untuk meningkatkan ketahanannya terhadap data yang bising (noisy) dan keberadaan outlier. Data di dunia nyata seringkali tidak sempurna, sehingga kemampuan algoritma untuk mengidentifikasi dan mengelola anomali data tanpa mengorbankan kualitas clustering akan menjadi kontribusi signifikan. Melalui eksplorasi ini, Iterative Grid Mapping K-Means berpotensi menjadi solusi clustering yang lebih kuat, adaptif, dan siap menghadapi tantangan data yang beragam.
| File size | 346.6 KB |
| Pages | 3 |
| DMCA | Report |
Related /
AREAIAREAI Temuan ini diharapkan dapat menjadi acuan bagi lembaga kepolisian dalam menciptakan kebijakan yang lebih inklusif dan responsif terhadap kebutuhan anggotaTemuan ini diharapkan dapat menjadi acuan bagi lembaga kepolisian dalam menciptakan kebijakan yang lebih inklusif dan responsif terhadap kebutuhan anggota
UMIUMI Perancangan sistem informasi penjualan pada Galeri Ulos ini diharapkan dapat memudahkan pelanggan mendapatkan informasi yang diinginkan. Perancangan sistemPerancangan sistem informasi penjualan pada Galeri Ulos ini diharapkan dapat memudahkan pelanggan mendapatkan informasi yang diinginkan. Perancangan sistem
UMIUMI Kuesioner tersebut berisi 20 pertanyaan. Selanjutnya data tersebut diolah dengan menggunakan metode Webqual 4. 0 dengan pemanfaatan aplikasi SPSS. SelainKuesioner tersebut berisi 20 pertanyaan. Selanjutnya data tersebut diolah dengan menggunakan metode Webqual 4. 0 dengan pemanfaatan aplikasi SPSS. Selain
UMIUMI Metode yang digunakan adalah tinjauan literatur komprehensif yang mengintegrasikan berbagai perspektif dan temuan empiris, serta analisis SWOT untuk mengevaluasiMetode yang digunakan adalah tinjauan literatur komprehensif yang mengintegrasikan berbagai perspektif dan temuan empiris, serta analisis SWOT untuk mengevaluasi
UMIUMI Dengan menyimpan referensi data (hash) pada blockchain dan log aktual pada IPFS, sistem memastikan pencatatan data yang dapat diandalkan, fleksibilitasDengan menyimpan referensi data (hash) pada blockchain dan log aktual pada IPFS, sistem memastikan pencatatan data yang dapat diandalkan, fleksibilitas
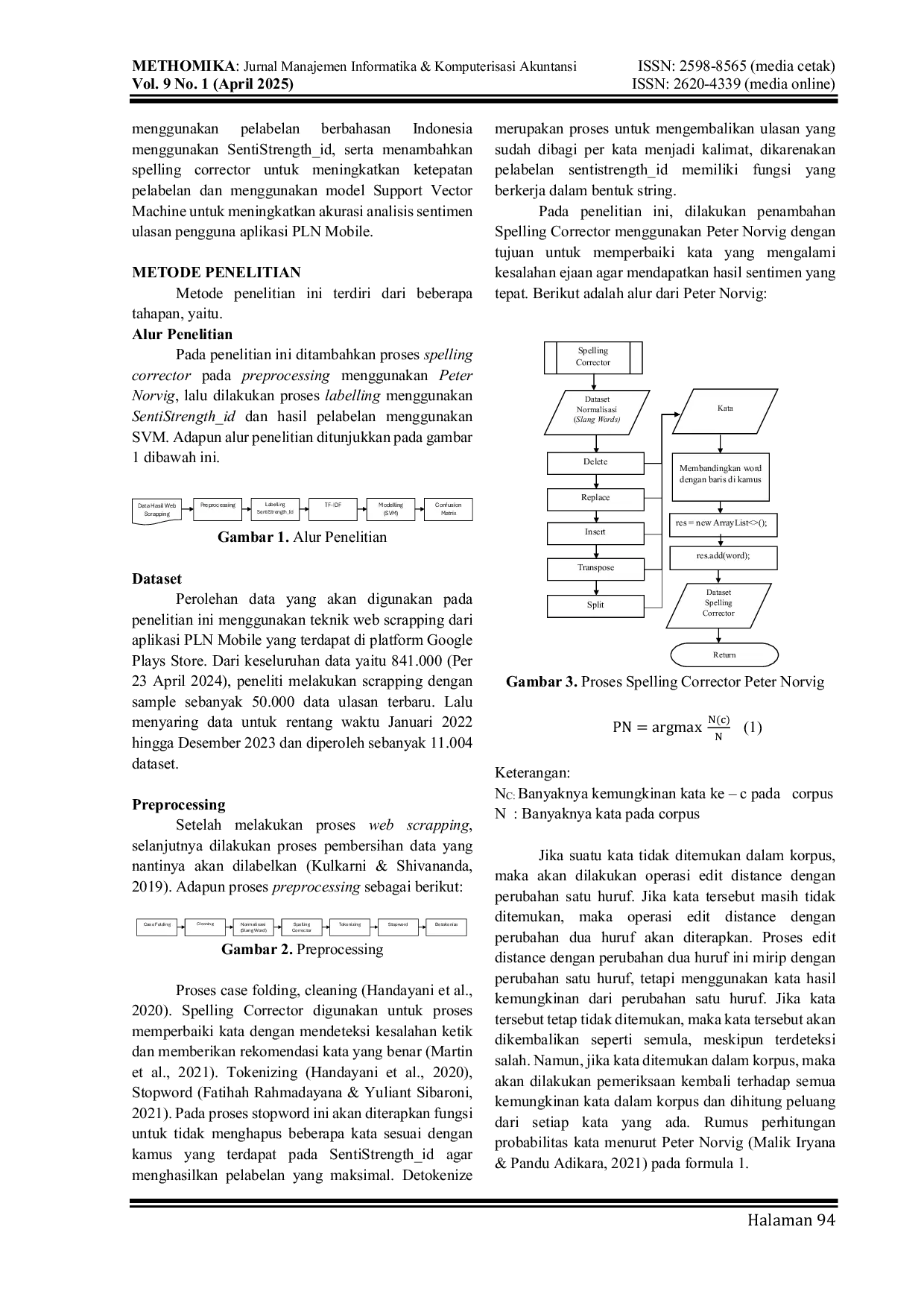
UMIUMI Penelitian ini menunjukkan bahwa implementasi Peter Norvig sebagai spelling corrector dalam tahapan preprocessing, bersama dengan metode SentiStrength_idPenelitian ini menunjukkan bahwa implementasi Peter Norvig sebagai spelling corrector dalam tahapan preprocessing, bersama dengan metode SentiStrength_id
UMIUMI Hasil akurasi yang kurang optimal untuk mendeteksi lebih dari 2 kelas disebabkan oleh variasi data yang kecil yang menyebabkan overfitting. Oleh karenaHasil akurasi yang kurang optimal untuk mendeteksi lebih dari 2 kelas disebabkan oleh variasi data yang kecil yang menyebabkan overfitting. Oleh karena
ALIMSPUBLISHINGALIMSPUBLISHING Tujuan penelitian ini untuk mendeskripsikan bentuk-bentuk interksi sosial dalam novel Rasa karya Tere Liye. Metode penelitian yang digunakan adalah deskriptifTujuan penelitian ini untuk mendeskripsikan bentuk-bentuk interksi sosial dalam novel Rasa karya Tere Liye. Metode penelitian yang digunakan adalah deskriptif
Useful /
AREAIAREAI Kinerja kontekstual adalah aspek penting dalam lingkungan kerja, yang mencerminkan perilaku sukarela karyawan atau pengusaha dalam membantu, berkolaborasi,Kinerja kontekstual adalah aspek penting dalam lingkungan kerja, yang mencerminkan perilaku sukarela karyawan atau pengusaha dalam membantu, berkolaborasi,
UMIUMI Penelitian ini menunjukkan bahwa algoritma Convolutional Neural Network (CNN) dengan arsitektur MobileNet efektif dalam mengklasifikasikan jenis sampahPenelitian ini menunjukkan bahwa algoritma Convolutional Neural Network (CNN) dengan arsitektur MobileNet efektif dalam mengklasifikasikan jenis sampah
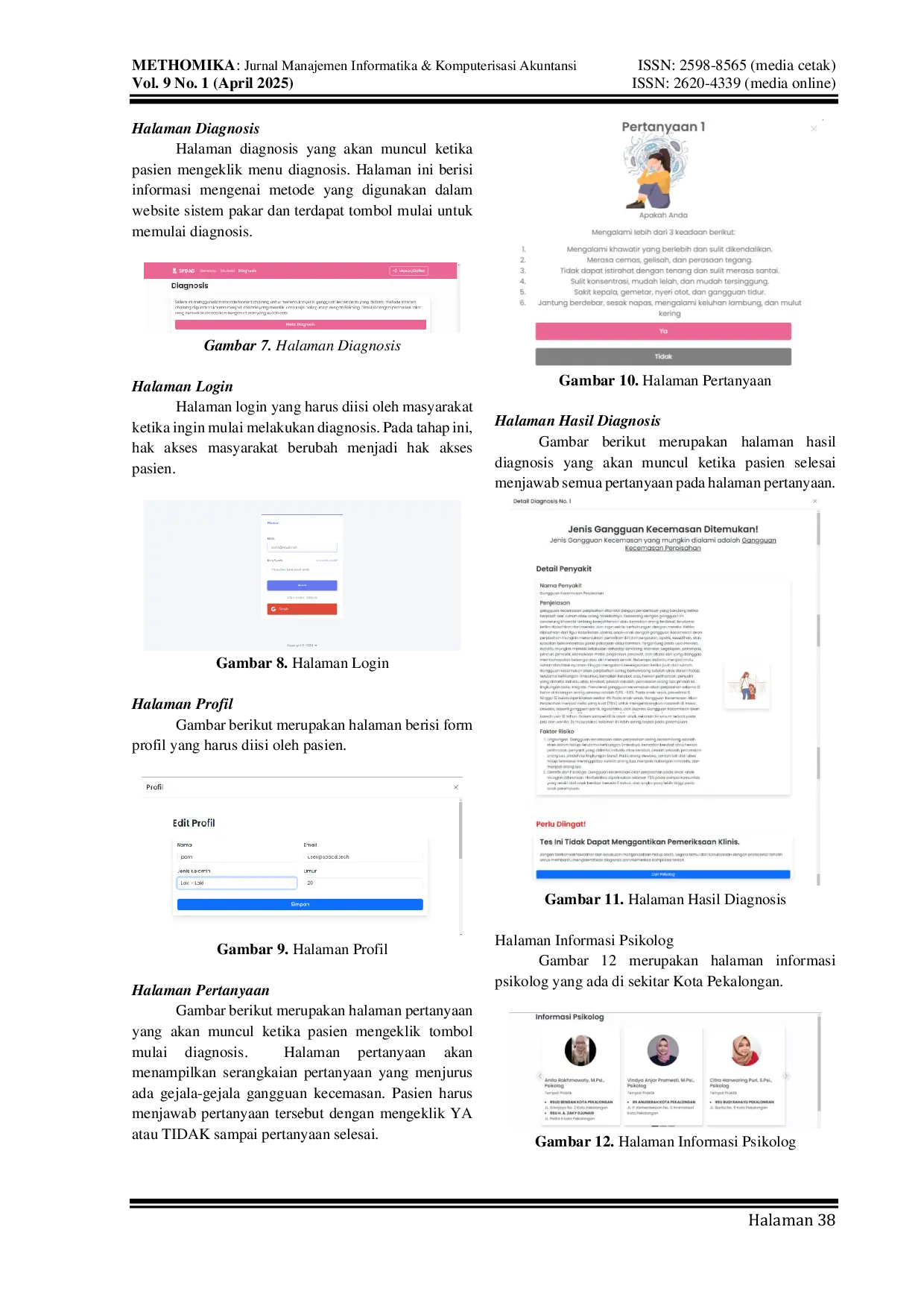
UMIUMI Gangguan Kecemasan adalah gangguan Kesehatan mental yang paling umum di dunia. Hasil Utama Riset Kesehatan RI 2018 menunjukkan peningkatan prevalensi gangguanGangguan Kecemasan adalah gangguan Kesehatan mental yang paling umum di dunia. Hasil Utama Riset Kesehatan RI 2018 menunjukkan peningkatan prevalensi gangguan
IAIN GORONTALOIAIN GORONTALO Artikel ini menganalisis faktor-faktor utama yang memengaruhi komunikasi, khususnya perbedaan budaya, perbedaan bahasa, dan perbedaan agama. Oleh karenaArtikel ini menganalisis faktor-faktor utama yang memengaruhi komunikasi, khususnya perbedaan budaya, perbedaan bahasa, dan perbedaan agama. Oleh karena