UNIDAUNIDA
Indonesian Journal of Applied Research (IJAR)Indonesian Journal of Applied Research (IJAR)Masalah transportasi (TP) merupakan faktor signifikan dalam riset operasional. Banyak peneliti telah mengemukakan berbagai solusi untuk masalah ini. Tujuannya adalah untuk mengurangi biaya total distribusi sumber daya dari beberapa sumber ke banyak destinasi. Jika terdapat risiko jalan (salju, banjir, dll), keterbatasan lalu lintas, dll, mungkin tidak memungkinkan untuk mengangkut produk dari satu tempat ke tempat lain. Dalam kondisi ini, rute yang sesuai dapat diberikan biaya satuan yang sangat tinggi, seperti M (atau ∞). Setelah itu, kasus khusus dari masalah transportasi dengan rute terlarang diperkenalkan. Oleh karena itu, fokus penelitian ini adalah untuk menyediakan algoritme baru yang akan mengurangi biaya masalah transportasi terbatas. Dengan beberapa modifikasi, pendekatan Vogel tradisional telah ditingkatkan. Metode yang diusulkan akan berkinerja lebih baik daripada pendekatan lain yang saat ini digunakan. Masalah numerik diselesaikan untuk mendemonstrasikan efektivitas pendekatan yang diusulkan dan membuat perbandingan dengan berbagai pendekatan yang telah ada.
Makalah ini mengusulkan metode baru, yaitu peningkatan metode aproksimasi Vogel, untuk menemukan solusi dasar yang efisien pada masalah transportasi dengan rute terlarang.Metode yang diusulkan diuji pada berbagai masalah transportasi, baik yang seimbang maupun tidak seimbang, dan hasilnya dibandingkan dengan solusi dari metode yang sudah ada untuk memeriksa efektivitasnya.Kesimpulannya, metode yang diusulkan terbukti memberikan solusi yang serupa atau lebih akurat dibandingkan metode lain, sehingga dapat dianggap sebagai pendekatan yang unggul untuk menyelesaikan masalah transportasi rute terlarang.
Penelitian ini telah berhasil menunjukkan metode baru untuk meminimalkan biaya pada jalur distribusi yang ada larangannya. Namun, masih banyak peluang untuk pengembangan lebih lanjut yang menarik. Pertanyaan penelitian pertama adalah, bagaimana cara kita mengembangkan algoritme ini agar tidak hanya memberikan solusi awal, tetapi juga bisa langsung menemukan solusi paling optimal tanpa perlu langkah tambahan, sehingga lebih efisien dalam satu paket terpadu? Kedua, penelitian selanjutnya bisa mengeksplorasi bagaimana metode ini dapat diadaptasi untuk menyelesaikan masalah yang lebih kompleks dengan lebih dari satu tujuan, seperti memilih rute yang paling murah dan tercepat secara bersamaan. Terakhir, sebuah arah studi yang sangat relevan adalah untuk mengujinya pada kondisi yang lebih dinamis, di mana sebuah jalan tidak benar-benar dilarang selamanya tetapi hanya memiliki risiko gangguan yang tinggi. Penelitian mendatang dapat mencari jawaban atas bagaimana cara memodifikasi algoritme agar dapat mempertimbangkan faktor ketidakpastian seperti risiko atau probabilitas gangguan, sehingga keputusan yang diambil lebih mencerminkan situasi yang sesungguhnya di lapangan.
| File size | 783.77 KB |
| Pages | 17 |
| DMCA | Report |
Related /
POLITEKNIKJAMBIPOLITEKNIKJAMBI Persediaan harus ditentukan terlebih dahulu sebelum penjualan dilakukan agar perusahaan dapat menentukan jumlah optimal persediaan barang sehingga jumlahPersediaan harus ditentukan terlebih dahulu sebelum penjualan dilakukan agar perusahaan dapat menentukan jumlah optimal persediaan barang sehingga jumlah
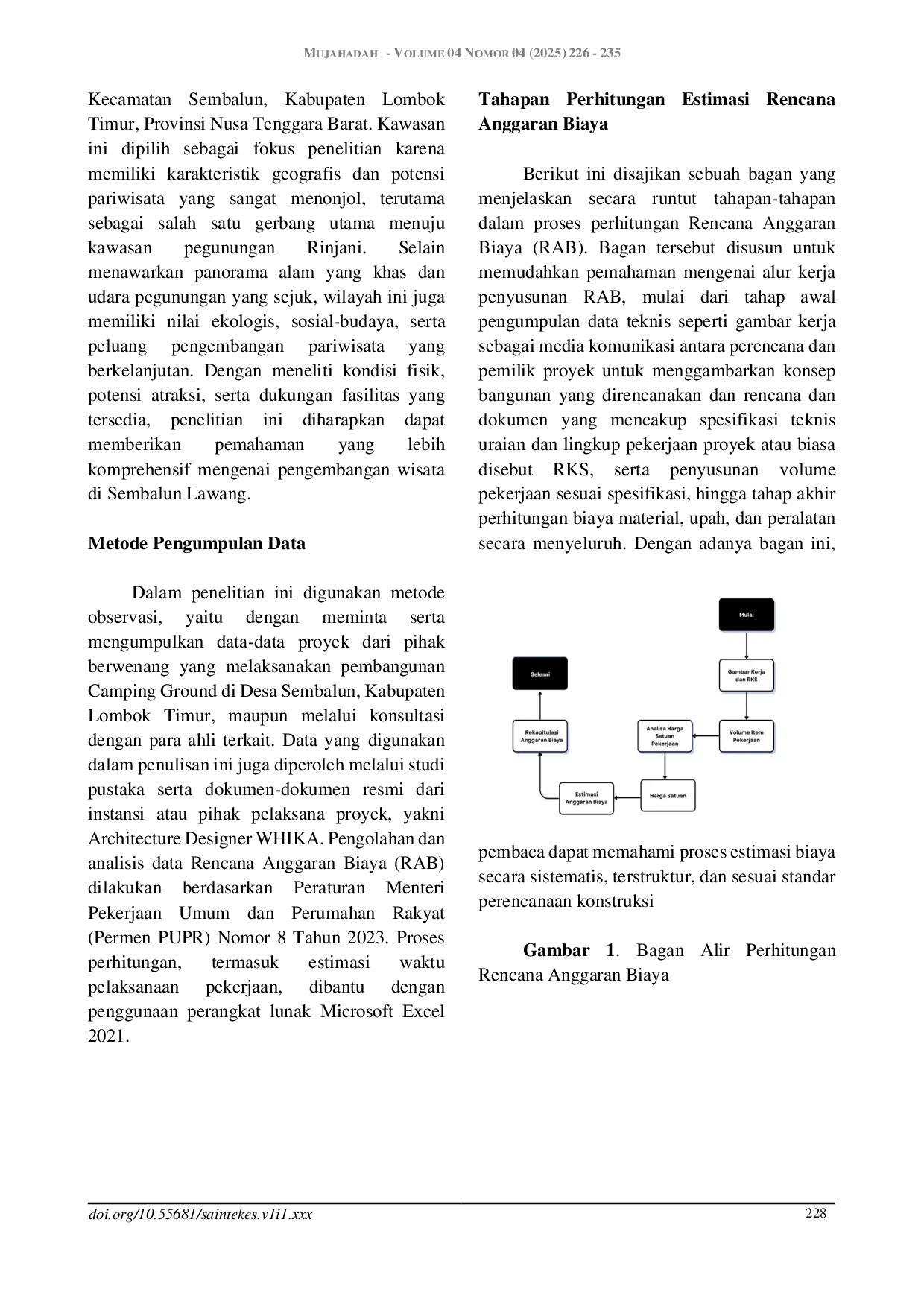
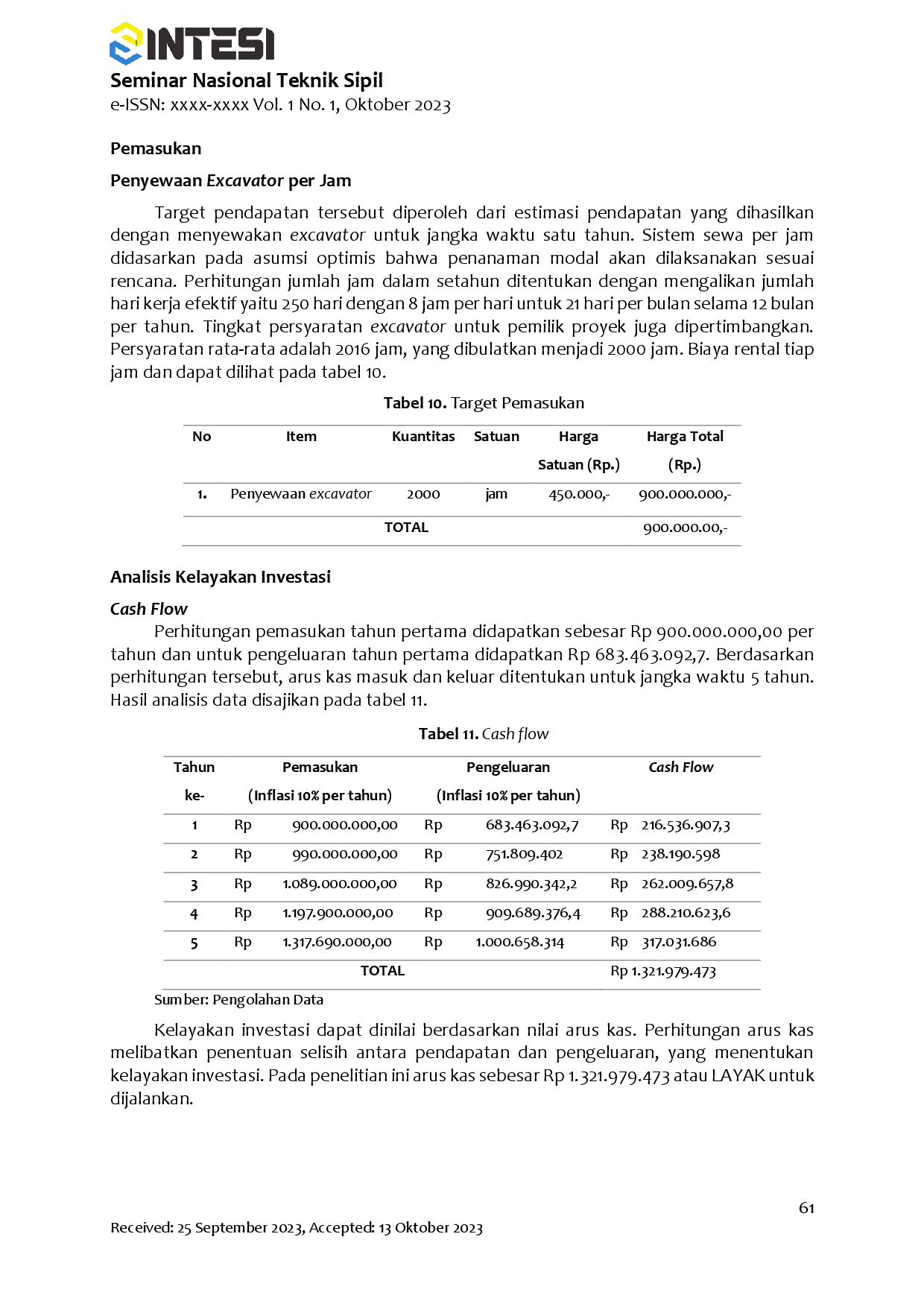
ITKAITKA Berdasarkan analisis metode SNI, total biaya pembangunan camping ground adalah Rp 1. 125.400.000,- (satu miliar seratus dua puluh lima juta empat ratusBerdasarkan analisis metode SNI, total biaya pembangunan camping ground adalah Rp 1. 125.400.000,- (satu miliar seratus dua puluh lima juta empat ratus
PUBLINEPUBLINE Perbedaan tersebut disebabkan oleh perbedaan konsep dalam menghitung biaya overhead pabrik, sehingga perhitungan menggunakan metode job order costing menghasilkanPerbedaan tersebut disebabkan oleh perbedaan konsep dalam menghitung biaya overhead pabrik, sehingga perhitungan menggunakan metode job order costing menghasilkan
AMSIRAMSIR As a recommendation, it is suggested to implement a hybrid trial model, which combines both online and offline hearings, to maintain a balance betweenAs a recommendation, it is suggested to implement a hybrid trial model, which combines both online and offline hearings, to maintain a balance between
AMSIRAMSIR Kedua sistem hukum tersebut menegaskan bahwa harta yang diperoleh selama perkawinan merupakan harta bersama yang pada dasarnya harus dibagi sama rata antaraKedua sistem hukum tersebut menegaskan bahwa harta yang diperoleh selama perkawinan merupakan harta bersama yang pada dasarnya harus dibagi sama rata antara
STIATA BALONGSTIATA BALONG 545.441.796 untuk 13.090 meter, dengan permintaan aktual 13.085 meter. Biaya produksi pagar adalah Rp 3. 146.436.796 untuk 6. 292 meter, dan railing tangga545.441.796 untuk 13.090 meter, dengan permintaan aktual 13.085 meter. Biaya produksi pagar adalah Rp 3. 146.436.796 untuk 6. 292 meter, dan railing tangga
IFRELIFREL Data were obtained through a literature review of academic books, scientific journals, and official documents relevant to the theme of curriculum and PAIData were obtained through a literature review of academic books, scientific journals, and official documents relevant to the theme of curriculum and PAI
EJOURNALUNIGOROEJOURNALUNIGORO Metode analisis data menggunakan analisis kelayakan investasi BCR (Benefit Cost Ratio). Berdasarkan hasil perhitungan, nilai produktivitas excavator PC195LC-8Metode analisis data menggunakan analisis kelayakan investasi BCR (Benefit Cost Ratio). Berdasarkan hasil perhitungan, nilai produktivitas excavator PC195LC-8
Useful /
ITKAITKA Kendala utama dalam implementasi strategi ini adalah rendahnya minat konsumsi masyarakat terhadap pangan non-beras dan terbatasnya akses pasar. TemuanKendala utama dalam implementasi strategi ini adalah rendahnya minat konsumsi masyarakat terhadap pangan non-beras dan terbatasnya akses pasar. Temuan
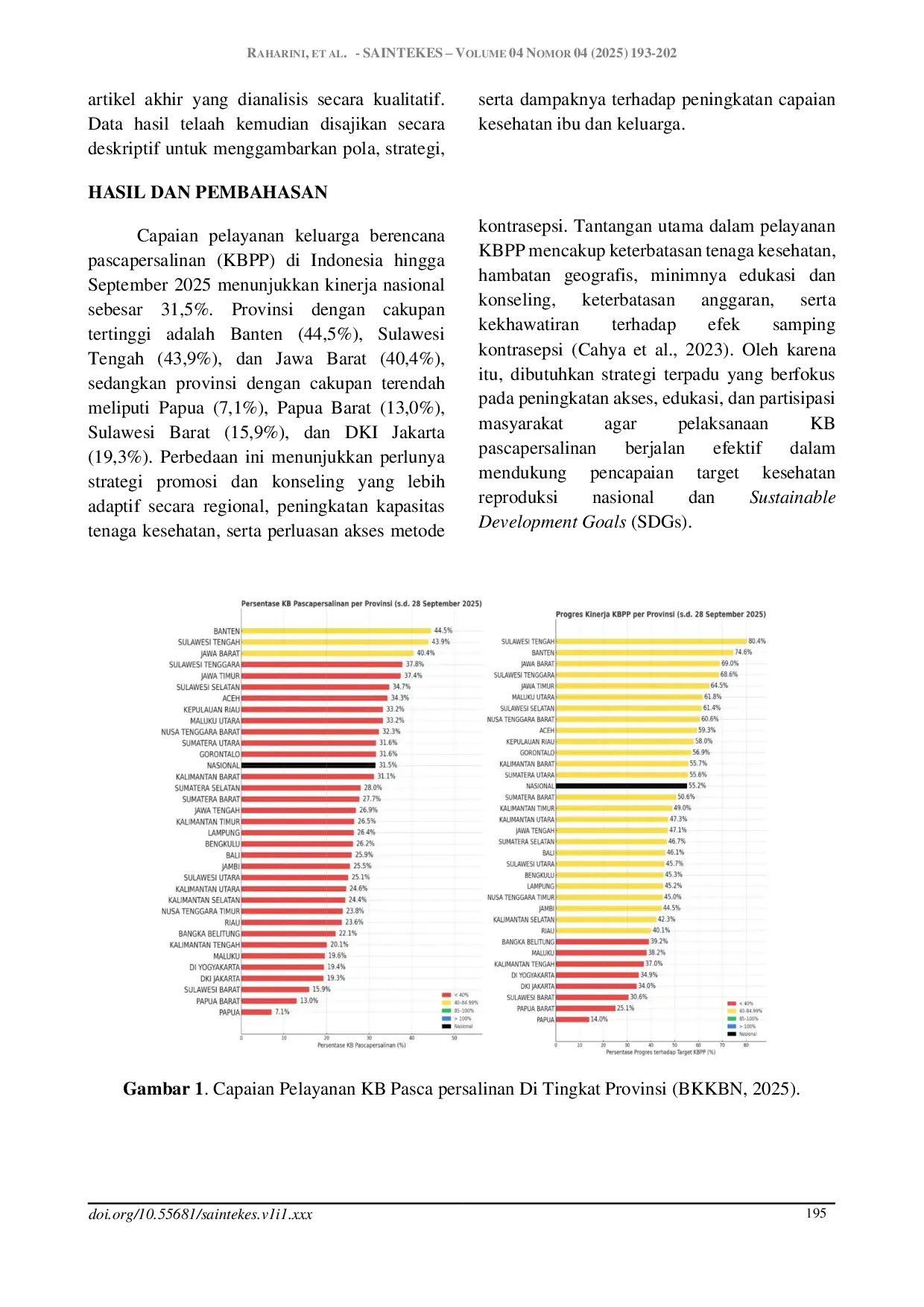
ITKAITKA Strategi yang kontekstual dan penguatan kapasitas tenaga kesehatan menjadi kunci keberhasilan program. Strategi promosi dan konseling kontrasepsi pascapersalinanStrategi yang kontekstual dan penguatan kapasitas tenaga kesehatan menjadi kunci keberhasilan program. Strategi promosi dan konseling kontrasepsi pascapersalinan
EJOURNALUNIGOROEJOURNALUNIGORO Kompleksitas Proyek, 8. Faktor Eksternal Proyek. Dari hasil variabel dan indikator dapat digunakan untuk mencari faktor dominan/tinggi dan juga strategiKompleksitas Proyek, 8. Faktor Eksternal Proyek. Dari hasil variabel dan indikator dapat digunakan untuk mencari faktor dominan/tinggi dan juga strategi
EJOURNALUNIGOROEJOURNALUNIGORO Hasil Penelitian menunjukkan bahwa analisis perhitungan dengan bantuan MSExcel dan hasil pemodelan dengan system fuzzy di aplikasi Matlab memberikan hasilHasil Penelitian menunjukkan bahwa analisis perhitungan dengan bantuan MSExcel dan hasil pemodelan dengan system fuzzy di aplikasi Matlab memberikan hasil