EJGTAEJGTA
Electronic Journal of Graph Theory and Applications (EJGTA)Electronic Journal of Graph Theory and Applications (EJGTA)Kertas ini merupakan tinjauan mengenai batas atas dan bawah untuk nilai eigen terbesar dari matriks Laplacian, yang dikenal sebagai jari-jari spektral Laplacian, dari suatu graf. Batas-batas tersebut diberikan sebagai fungsi dari parameter graf seperti jumlah simpul, jumlah sisi, derajat simpul, rata-rata derajat 2, diameter, nomor penutupan, nomor dominasi, nomor independensi, dan parameter lainnya. Tinjauan ini mencakup berbagai hasil penelitian tentang batas-batas ini, termasuk kondisi yang memungkinkan kesamaan batas dan aplikasinya dalam bidang seperti optimisasi kombinatorial, jaringan komunikasi, dan kimia teoretis.
Penelitian ini meninjau berbagai batas atas dan bawah untuk jari-jari spektral Laplacian dari graf, dengan fokus pada parameter graf seperti jumlah simpul, derajat, dan struktur.Berbagai batas ini memberikan wawasan tentang sifat-sifat struktural graf melalui analisis nilai eigen matriks Laplacian.Hasil penelitian ini dapat digunakan untuk memahami lebih baik hubungan antara struktur graf dan sifat-sifat spektralnya.
1. Mempelajari batas untuk jari-jari spektral Laplacian pada graf dinamis atau graf berbobot yang belum sepenuhnya diteliti. 2. Membandingkan efektivitas berbagai batas dalam aplikasi nyata seperti jaringan komunikasi atau kimia teoretis. 3. Mengembangkan algoritma komputasi untuk mengevaluasi batas-batas ini secara efisien pada graf besar.
| File size | 364.25 KB |
| Pages | 28 |
| DMCA | ReportReport |
Related /
IPBIPB Hutan perkotaan merupakan infrastruktur hijau penting yang menyediakan berbagai layanan lanskap, termasuk pengikatan karbon, pengaturan mikroiklimat, danHutan perkotaan merupakan infrastruktur hijau penting yang menyediakan berbagai layanan lanskap, termasuk pengikatan karbon, pengaturan mikroiklimat, dan
IPBIPB Sampel terdiri dari tiga puluh delapan (38) rumah walet yang berada di wilayah ekologi pesisir, perbukitan, dan dataran pada kabupaten‑kabupaten di ProvinsiSampel terdiri dari tiga puluh delapan (38) rumah walet yang berada di wilayah ekologi pesisir, perbukitan, dan dataran pada kabupaten‑kabupaten di Provinsi
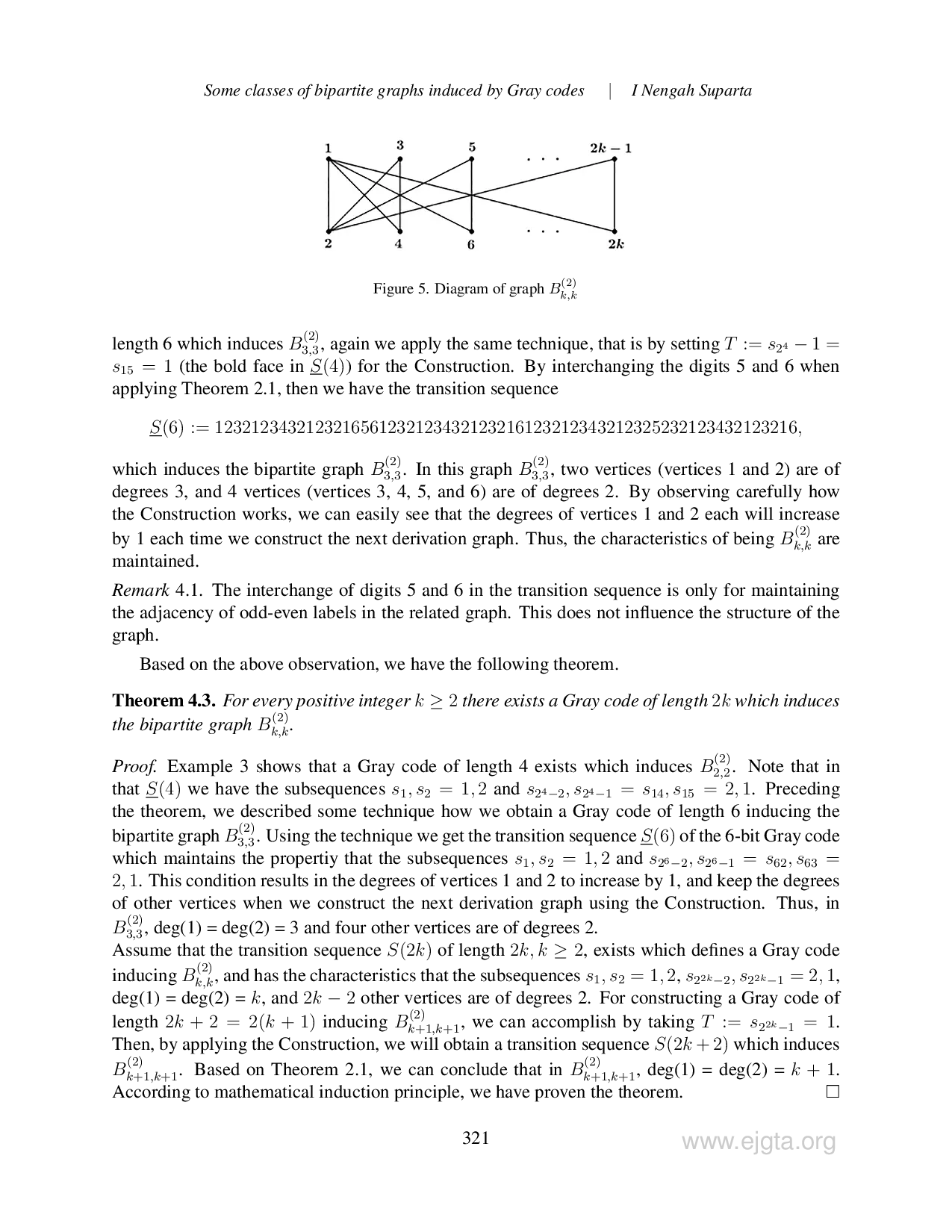
EJGTAEJGTA Jika kata code pertama dan terakhir juga memiliki sifat tersebut, Gray code disebut siklik, sebaliknya disebut non-siklik. Angka yang menunjukkan posisiJika kata code pertama dan terakhir juga memiliki sifat tersebut, Gray code disebut siklik, sebaliknya disebut non-siklik. Angka yang menunjukkan posisi
IAESCOREIAESCORE Citra hasil campuran dibagi menjadi blok-blok berukuran 8x8. Blok-blok ini juga diacak untuk mencapai tingkat kebingungan yang baik. Untuk meningkatkanCitra hasil campuran dibagi menjadi blok-blok berukuran 8x8. Blok-blok ini juga diacak untuk mencapai tingkat kebingungan yang baik. Untuk meningkatkan
Useful /
RESEARCHSYNERGYPRESSRESEARCHSYNERGYPRESS Dengan mengotomatisasi proses pengambilan keputusan, sistem ini meningkatkan efisiensi dan akurasi, memungkinkan administrator dan pendidik membuat keputusanDengan mengotomatisasi proses pengambilan keputusan, sistem ini meningkatkan efisiensi dan akurasi, memungkinkan administrator dan pendidik membuat keputusan
RESEARCHSYNERGYPRESSRESEARCHSYNERGYPRESS Bukti eksperimental mengkonfirmasi perbaikan yang signifikan dalam ketepatan rekomendasi dan metrik kepuasan pengguna dengan sistem rekomendasi yang ditingkatkan.Bukti eksperimental mengkonfirmasi perbaikan yang signifikan dalam ketepatan rekomendasi dan metrik kepuasan pengguna dengan sistem rekomendasi yang ditingkatkan.
UNUDUNUD Penelitian ini memeriksa revitalisasi tari Sanghyang Grodog di Desa Lembongan, Bali, menggunakan pendekatan socio-artisistik yang didukung teori kohesiPenelitian ini memeriksa revitalisasi tari Sanghyang Grodog di Desa Lembongan, Bali, menggunakan pendekatan socio-artisistik yang didukung teori kohesi
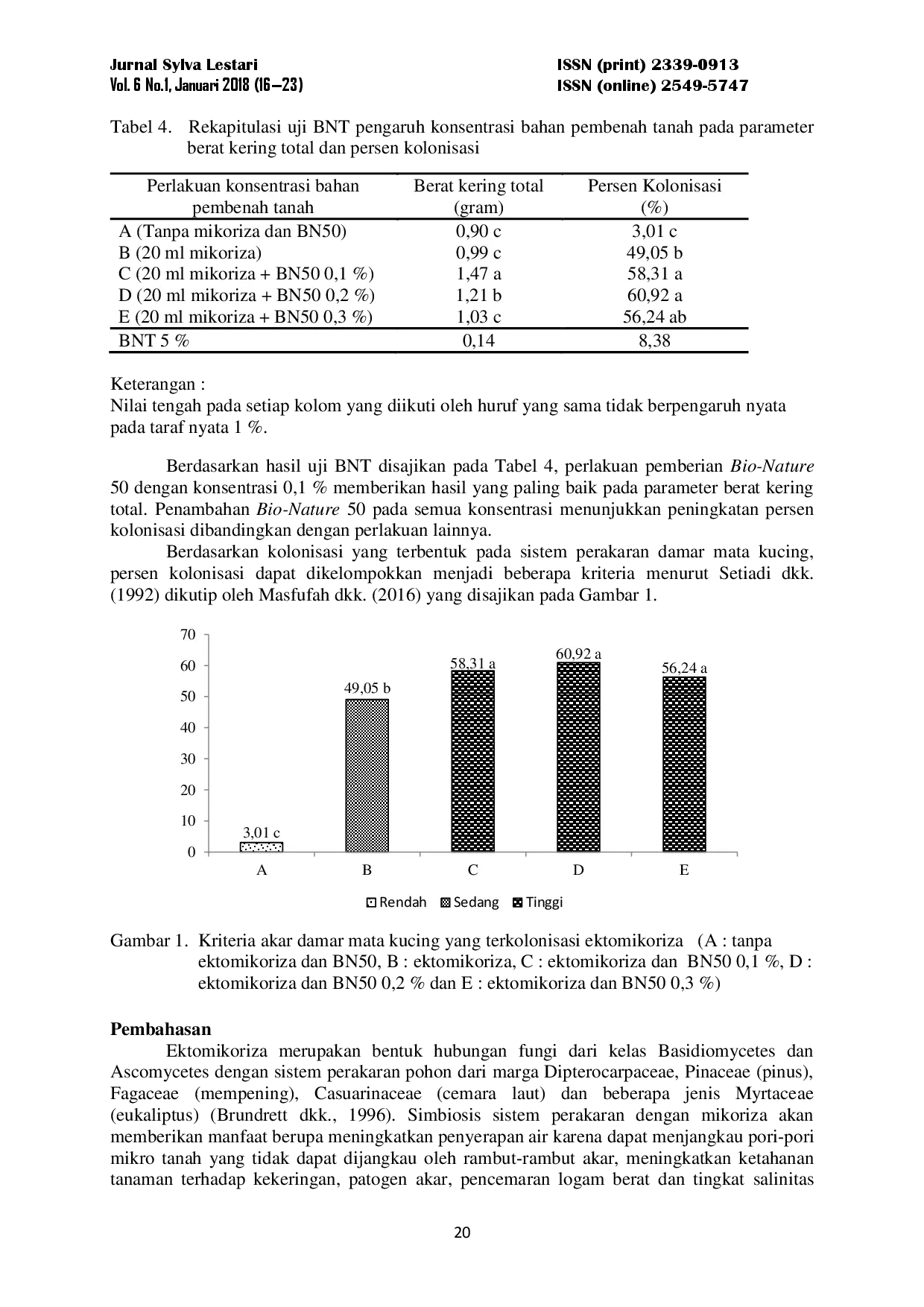
UNILAUNILA Pemberian Bio-Nature 50 dengan konsentrasi 0,1 %, 0,2 % dan 0,3 % pada media yang telah diinokulasikan ektomikoriza memberikan hasil yang sama baiknyaPemberian Bio-Nature 50 dengan konsentrasi 0,1 %, 0,2 % dan 0,3 % pada media yang telah diinokulasikan ektomikoriza memberikan hasil yang sama baiknya